Current open source slicers for 3D-Printers such as slic3r or CuraEngine divide objects into a set of equally thick layers, where the value for the layer height is given by the user. This is just fine for many applications, as it gives the most equally structured surface.

The idea to determine the layer height automatically by analyzing the structure of the surface in the objects current region has been lingering around in the scientific community for about 2 decades now. Slicing with thick layers results in a surface like this:

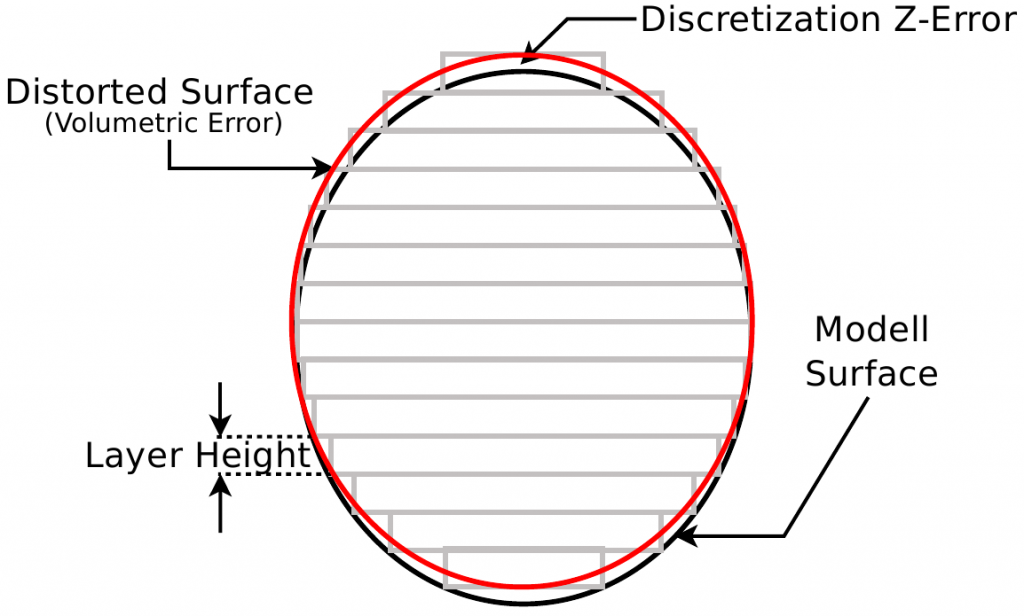The steeper slopes in the top and bottom of the object heavily suffer from “stair-stepping”, where the surface can only be roughly approximated by 2D slices. To avoid this, the layer height can be reduced depending on the angles of the corresponding surface facets in the models tessellation data. The cusp value has been introduced as an error measure to calculate the actual layer height:

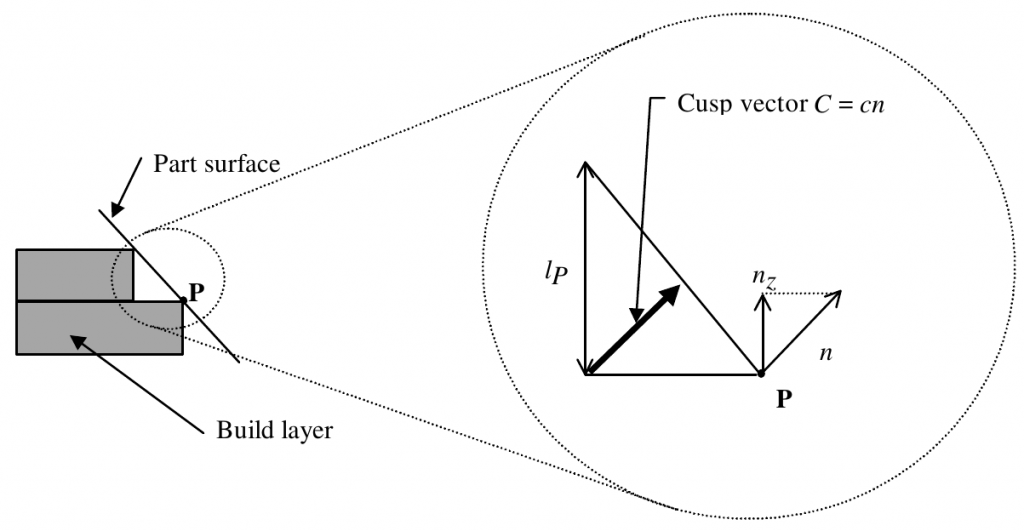
Image from: DOLENC , A. und I. MÄKELÄ: Slicing procedures for layered manufacturing techniques. Computer-Aided Design, 26(2), 1994

The cusp vector C describes the maximum distance between the desired surface of the model and the (simplified) resulting printed surface. C has to be maintained below a certain user defined value C_max, which describes the maximum allowed deviation between printed- and model-surface. To achieve this, c can be computed by simply dividing C_max/n_z where n_z is the z-component of the surface normal. Since C would become infinitely high for vertical surfaces, the printers technical layer height limit L_max (~nozzle diameter) must be known and c is computed as c = min{L_max, C_max/n_z} for a single facet.

The result is clearly visible in the following Image: the feet of both objects are printed with 0.4mm thickness, the slope of the left block is reduced by the algorithm to fit an error of C_max = 0.15, as a result, the layer height rises during the slope and the upper part is again printed with 0.4mm.

The left object is adaptively sliced, the right one static. Both with a maximum layer thickness of 0.4mm.

Implementation Details

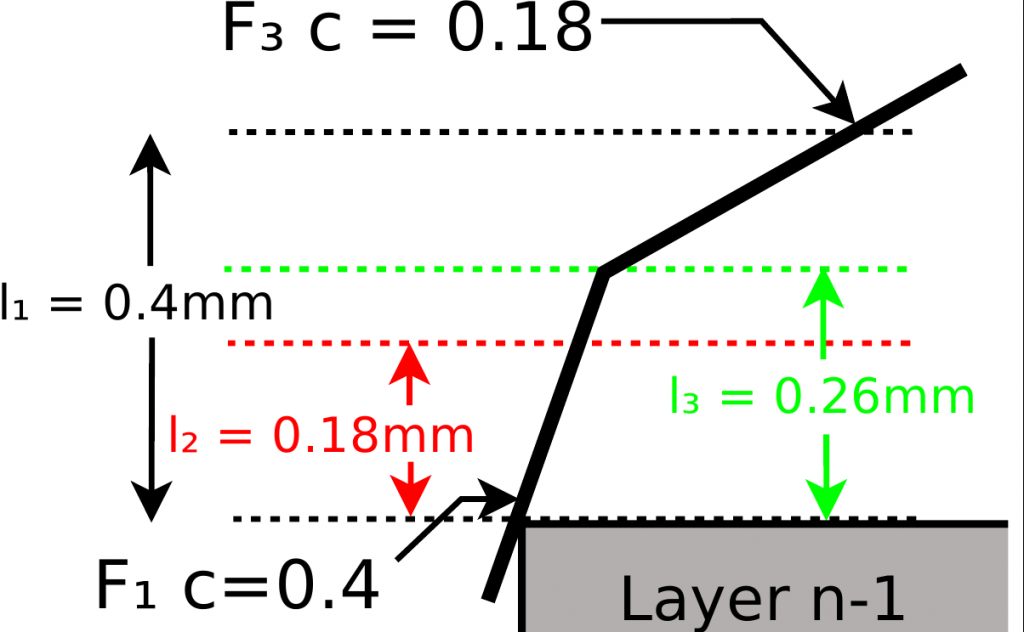
For a given layer, the intersection between the horizontal plane representing the layer and the facets can be computed basically at 3 positions:

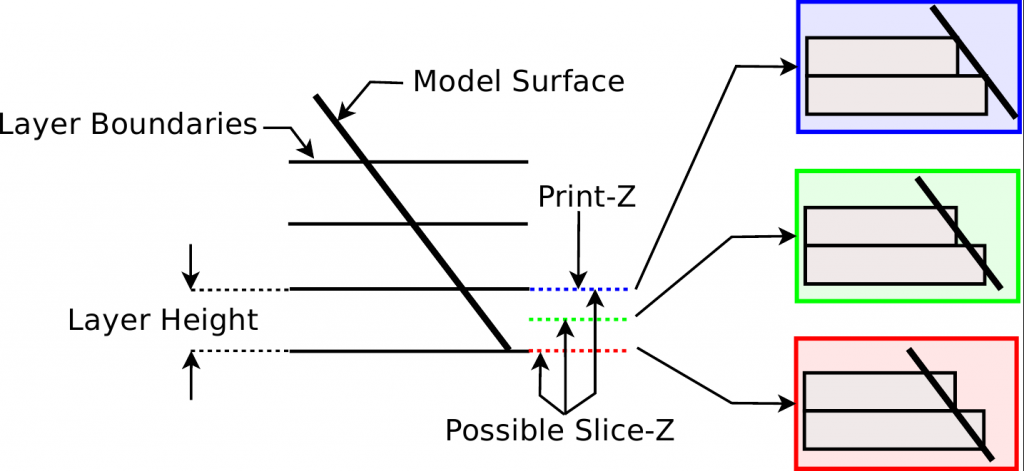The obvious approach is to use do the intersection in the middle of each layer (green line) to equally distribute the deviation independent of whether the surface is “rising” or “falling”. To get the Cusp height correct, every facet intersecting a given layer at any height has to be analyzed, without knowing the actual height in the beginning of the process. This could be done by using the printers maximal layer height as an upper limit and reducing the layer height during the process. However, in some cases the result would be non optimal. Consider a case of a nearly horizontal facet directly on top of a nearly vertical facet.

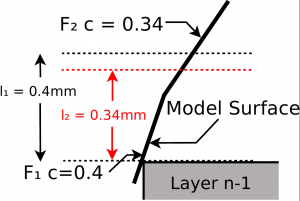
In the left case, the lowest cusp value (0.34mm) is optimal. In the right case, the upper facet would reduce the layer height to 0.18mm (red line), resulting in a layer that would not even touch the facet in question. To avoid this, the layer height should be reduced to the lowest point of F₃ (Z_min) only.

The implementation I’ve done for Slic3r computes the cusp value for every facet intersecting the lowest slice-z plane (the red one) in a first iteration and cycles through every remaining facet touching the layer from the first iteration in a second run, reducing the layer height to max(c, Z_min) if necessary.

For further reading please take a look into my master thesis (German only).

This work, unless otherwise expressly stated, is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.